The Art of Estimation, Left vs. Right Endpoint Sums for Area Calculation
When diving into the world of calculus, one of the fundamental concepts you’ll encounter is the concept of approximating the area under a curve using sums. Two common types of approximations are left endpoint sums and right endpoint sums. These techniques play a crucial role in understanding integration and the behavior of functions.
The Basics of Sums and Approximations
Imagine you have a curve on a graph, representing a function. The area under this curve between two points on the x-axis holds valuable information about the behavior of the function. But how do we calculate this area when the curve isn’t easily described by a simple mathematical formula?
That’s where approximations come in. By dividing the interval between two x-values into smaller subintervals, we can treat each subinterval as a rectangle and calculate the combined area of these rectangles to approximate the total area under the curve.
Left Endpoint Sums
A left endpoint sum, also known as a left Riemann sum, approximates the area under the curve using the left endpoint of each subinterval. Here’s how it works:
- Divide the interval \([a, b]\) into smaller subintervals of equal width.
- For each subinterval, find the height of the rectangle by evaluating the function at the left endpoint of the subinterval.
- Calculate the area of each rectangle by multiplying its height by the width of the subinterval.
- Add up the areas of all the rectangles to approximate the total area under the curve.
Mathematically, the left endpoint sum for a function \(f(x)\) over the interval \([a, b]\) with \(n\) subintervals is given by:
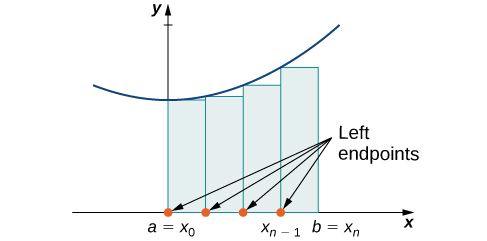
where \(\Delta x\) is the width of each subinterval.
Right Endpoint Sums
On the other hand, a right endpoint sum, or a right Riemann sum, approximates the area under the curve using the right endpoint of each subinterval. The process is similar to the left endpoint sum, but the heights of the rectangles are determined by evaluating the function at the right endpoints of the subintervals.
Mathematically, the right endpoint sum for a function \(f(x)\) over the interval \([a, b]\) with \(n\) subintervals is given by:
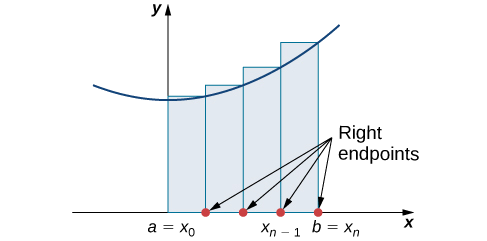
Comparing Left and Right Endpoint Sums
Left and right endpoint sums provide two different ways to approximate the area under a curve. Depending on the behavior of the function, the two approximations might yield slightly different results. In some cases, they might even converge to the actual area as the number of subintervals increases.
It’s important to note that both left and right endpoint sums are types of Riemann sums, which are foundational to understanding the concept of integration. As you delve deeper into calculus, you’ll discover that the definite integral of a function is the limit of these Riemann sums as the width of the subintervals approaches zero.
Conclusion
Left endpoint and right endpoint sums are valuable tools in the calculus toolkit. They provide a way to approximate the area under a curve when the function isn’t easily integrated. These concepts pave the way for understanding integration, the fundamental theorem of calculus, and more advanced topics in calculus.
By grasping the fundamentals of left and right endpoint sums, you’re taking the first steps toward a deeper comprehension of the intricate relationships between functions, their derivatives, and the areas they enclose.
So the next time you encounter a curve that seems elusive to integrate directly, remember that left and right endpoint sums are there to help you approximate and gain insights into its behavior.